Electrodialysis

Measurement of an Eddy Diffusivity for Chaotic Electroconvection

1. Motivation

Hydrodynamic instability of electrolytes near ion-selective membranes or electrodes may give rise to electroconvection, a vortical flow that substantially influences the transport of solutes in membrane-based synthesis and separation processes and electrochemical cells featuring electrodeposition [1]. At high current density/voltage, the flow transitions into the chaotic regime, exhibiting unsteady fluctuations with broadband spectra [2]. After averaging in time and in statistically homogeneous spatial directions, however, the resulting mean concentration and electric potential profiles are smooth and 1D while still permitting calculation of mean cell voltage and current. We propose a method to enable direct computation of the mean concentration and potential profiles without expensive 3D simulations.

Publications:

Phys. Rev. Fluids (2024)

Collaborators:

2. Reynolds-averaged Equations

The Poisson-Nernst-Planck-Stokes (PNPS) equations are known to capture the dynamics of chaotic electroconvection accurately [1]. Though Reynolds averaging [3] may be used to derive governing equations for the mean concentration and electric potential fields, solution of the equations is stymied by the presence of unclosed, Reynolds-stress-like terms.

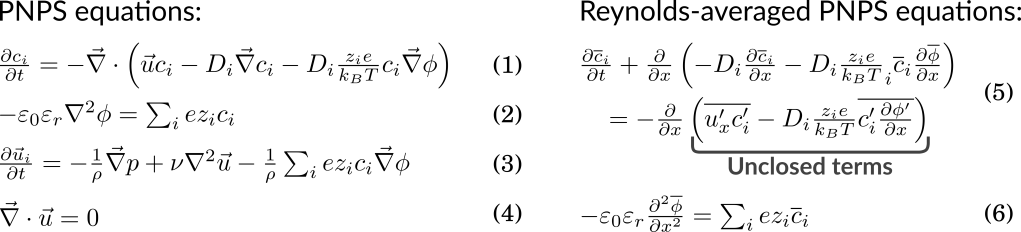
3. Micro-PTV Experiments

We perform microparticle tracking velocimetry (μ-PTV) experiments [4] to measure 3D, space-time-resolved velocity fields for use in our numerical procedure (the Macroscopic Forcing Method), circumventing the need for expensive 3D simulations.

4. Macroscopic Forcing Method

5. Eddy Diffusivity Profiles

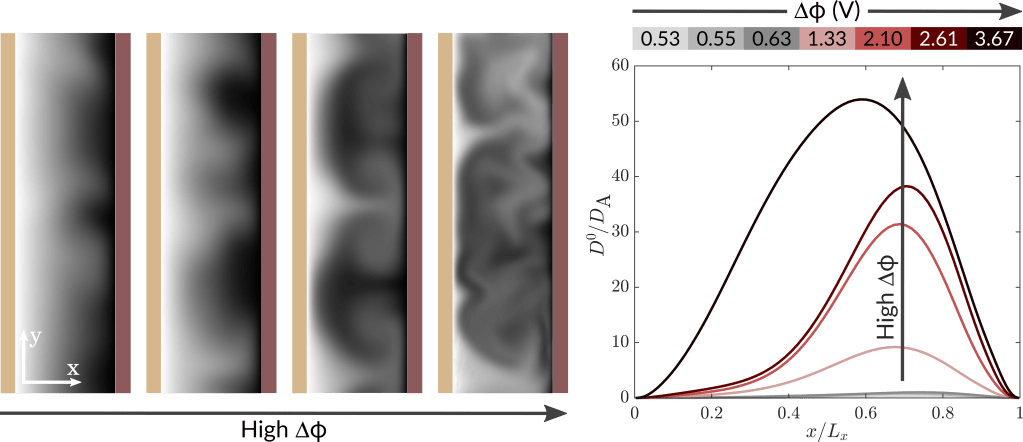
We implement the Macroscopic Forcing Method for a set of cases with different cell voltages. Two-dimensional slices of salt concentration reveal that mixing is more vigorous at higher voltage. This well-known result is seen in the measured eddy diffusivity profiles, which have larger magnitude at higher voltages.

6. Directly-computed Mean Profiles

The leading-order closure model and measured eddy diffusivity may be incorporated into eq. (5), resulting in the well-known 1D Poisson-Nernst-Planck (PNP) equations, in which the effects of chaotic electroconvection are now represented wholly by the eddy diffusivity. We may now perform steady 1D simulations to directly solve for the mean concentration and potential profiles, substantially reducing cost compared to unsteady 3D simulations. Furthermore, we show via comparison against 3D salt transport simulations that the leading-order closure model is sufficient to yield excellent agreement.

7. Current-voltage Curves

We compute the mean current density from the mean concentration and electric potential fields. The resulting current-voltage curve is plotted alongside experimental current-voltage measurements, demonstrating excellent agreement.

References

[1] Mani, A. and Wang, K. M., Annu. Rev. Fluid Mech., 52 509-529, (2024)
[2] Druzgalski, C. and Mani, A., Phys. Rev. Fluids, 1 073601, (2016)
[3] Pope, S. B., Turbulent Flows (Cambridge University Press, 2000)
[4] Stockmeier, F. et al., J. Membr. Sci., 640 119846, (2021)
[5] Mani, A. and Park, D., Phys. Rev. Fluids, 6 054607 (2021)

Acknowledgements

This work was supported by the National Science Foundation under grant 1553275, the Office of Naval Research, and the Department of Energy under grant DE-SC0021633. A.B. was additionally supported by the Charles H. Kruger Stanford Graduate Fellowship. F.S. was supported by a Fulbright Fellowship.

Material on this page was presented as a contributed poster at the ELKIN 2024 Conference. The full citation for the poster is:

A. Balaji-Wright, F. Stockmeier, R. Dunkel, M. Wessling, and A. Mani, “Measurement of an eddy diffusivity for chaotic electroconvection,” presented at the 15th Meeting of the International Electrokinetics Society, Sevilla, ESP, 2024.